Swapping Self-Attention with Fourier Transforms

Table of Contents

1. Introduction
2. Hypothesis
3. Experiment
4. Assumptions and tools
5. Why FFT ensures token mixing
6. Fine-tuning on IMDb binary classification (GPU)
7. Results — BERT-Tiny (vanilla)
8. Results — FNet-BERT-Tiny
9. Time required for training
10. Fine-tuning on IMDb binary classification (CPU)
11. Graphical results
12. Conclusion
13. Inference time
14. Training time
15. Accuracy
16. FNet variations
17. References

Introduction

This is an experiment to speed up traditional transformer based encoders, with limited accuracy cost, by replacing the self attention layer with 2D fourier transform.

Self attention provides a way to "mix" the input tokens, so that we can establish relationships between each token of the input. Since each token interacts with all the other tokens, the time complexity for such operation is O(n2). There have been many alternatives to reduce this complexity, one such almost radical work is to use fourier transform instead. In a Fourier transform based language model one learning layer is reaplce with a fixed (non-learnable) fucntion, which ensures the 'mixing' of tokens. For this experiment I will apply a 2d transform across the two input dimensions ie. $(sequence-length, hidden- dimenension)$ just like the FNet- original paper.

Hypothesis

Can this neural net architecture:

1. Reduce finetuning/training time becuase of reduced total learnable paramaters, since unlike self attention we are not learning the weights (and biases!)
2. Shave off inference time (lets say by ~10 percent) yet being usable (acccuracy ~90%) wrt. the original model.

The realtive training, inference time and performace will vary based on the implementation of the 2D fourier transform (There are many FFT algorithms). For this experiment I am using the FFT module present in pytorch. An extension of this expeirment can be to compare different FFT algortihms across devices (GPU, CPU, TPU).

Experiment

Assumptions and tools

• Using a small embedding model like bert-tiny
• Only swap the self attenions layer with 2d fourier transform, keeping the rest identical to the base model ie. bert-tiny
• There are many implementations of the FFT (fast fourier transform) alogrithm. I will rely on the torch implementation for FFT.
• Intuitively the fouruier transform will decompose the input signal of shape $(sequence-length , hidden-dimension)$ into the frequency domain, which will be passed on to the next layer.
• Test on simple NLP task like binary classification - imdb.
• There are many implemetations of doing a 2D fourier transform. For this experiment I will be using this implemetation inspired from the orignal Fnet paper.

class FNetBlock(nn.Module):
"""The FNet block which replaces the self-attention layer."""
def __init__(self):
    super().__init__()

def forward(self, hidden_states, attention_mask=None, head_mask=None,
            encoder_hidden_states=None, encoder_attention_mask=None,
            past_key_value=None, output_attentions=False):
    # Apply 2D FFT and take the real part. The output is a single tensor.
    return (torch.fft.fft(torch.fft.fft(hidden_states, dim=-1), dim=-2).real,)

The first FFT is applied across the sequence length dimension and the second transform is applied across the hidden dimension, and only the real part of the final output ie. the frequencies tensor is considered (although magnitude of each frequency should work, albeit with more computation overhead). The frequencies tensor is of shape $(sequence-length, hidden-dimension)$; this ensures that we can swap the attention layer without touching any other layers.

Please note: Fast Fourier Transform (FFT) is the name of the algorithm that computes the Discrete Fourier Transform (DFT). FFT uses divide and conquer approach to reduce the time complexity to $Nlog(N)$. Also, pytorch has inbuilt support for 2D FFT using torch.fft.fft2, but for this experiment I am chaining together the operations and taking the real part of each fourier frequency (as shown in FNetBlock).

Why FFT ensures token mixing?

2D FFT across $(sequence-lenth, Hidden-dimnesion)$ means 1D FFT across all the rows, and 1D FFT across all the columns. $$ X_k = \sum_{n=0}^{N-1} x_n \cdot e^{-i \frac{2\pi}{N} kn} $$

Where:

• $X_k$ is the k-th frequency element of the frequqency tensor(the output).
• $x_n$ is the n-th sample in the time-domain sequence (the input).
• $N$ is the total number of samples.
• $n$ is the current sample index, from $0$ to $N-1$.
• $k$ is the current frequency index, from $0$ to $N-1$.
• $i$ is the imaginary unit, where $i^2 = -1$.
• $e$ is Euler's number.

Each element of the Frequency tensor $X_k$ is the function of summation of all the elements in $x$. This ensures mixing of the individual elements of input tensor $X$.

An exmaple of applying fourier transform

Fine-tuning on IMDb binary classification (GPU)

IMDb is a small dataset for classifying sentiments (positive or negative) based on a text. I will use this data to test out the hypothesis.

Throught the experiment, the validation loss is consistantly going up after the 6th/7th epoch, however for brevity I will only choose the best performing model based on accuracy irrespective of it midly overfitting on the train data.

Results — BERT-Tiny (vanilla)

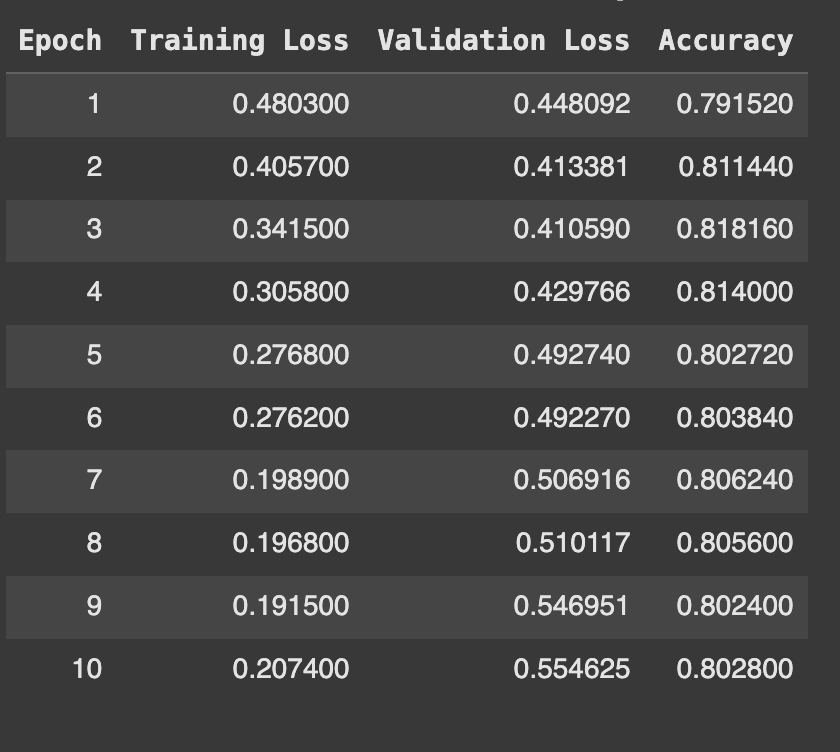Vanilla-Bert-Tiny trained on GPU - Train, validation loss and accuracy on finetuning on the IMDB dataset.

Results — FNet-BERT-Tiny

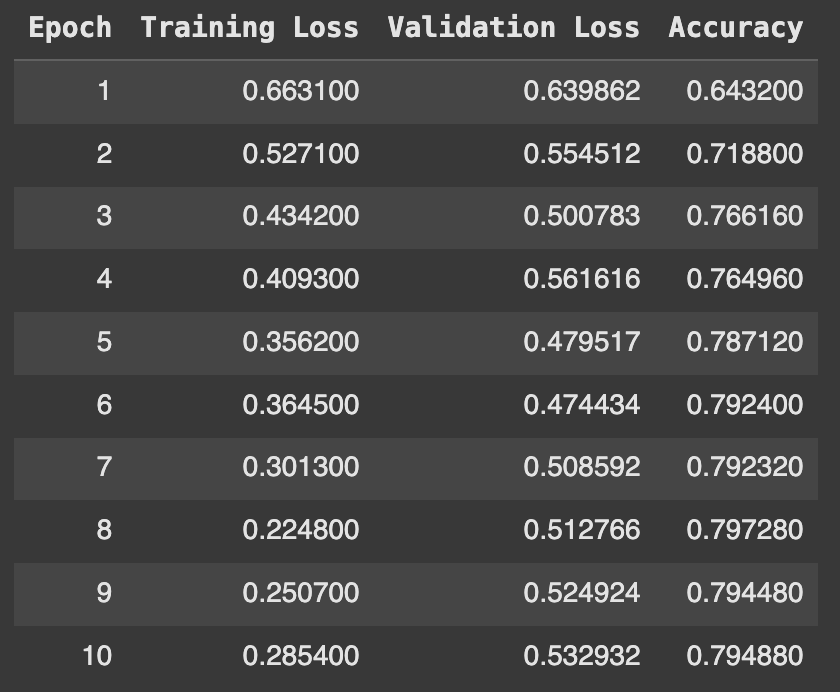Fnet-Bert-Tiny trianed on GPU - Train, validation loss and accuracy on finetuning on the IMDB dataset

Time required for training

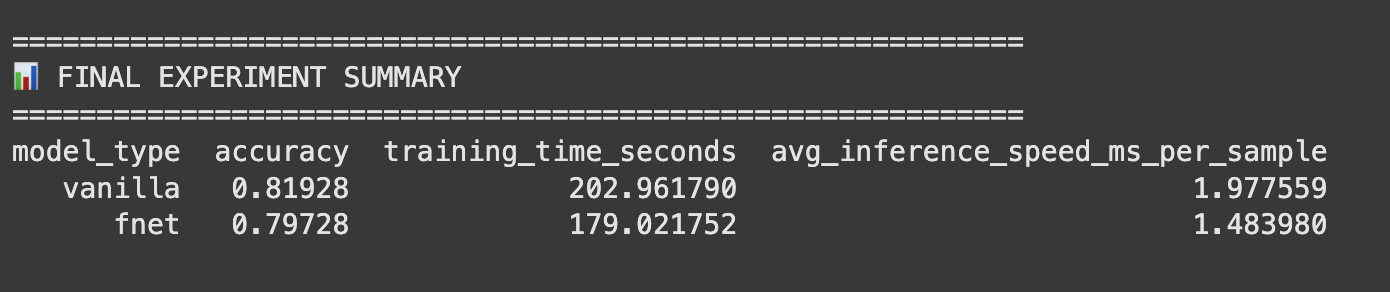Fnet-Bert-Tiny and bert-tiny (vanilla) on GPU - Training and inference time

Similar to Vanilla-Bert-Tiny finetuning, the Fnet variant also exhibits spike in validation loss after the 7th/8th epoch.

Fine-tuning on IMDb binary classification (CPU)

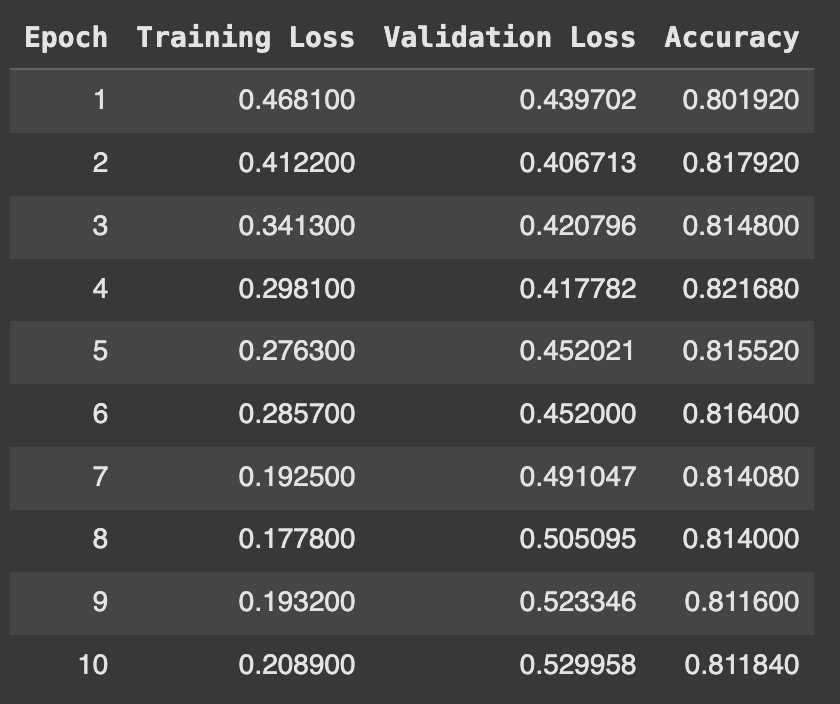Vanilla-Bert-Tiny trined on CPU - Train, validation loss and accuracy on finetuning on the IMDB dataset

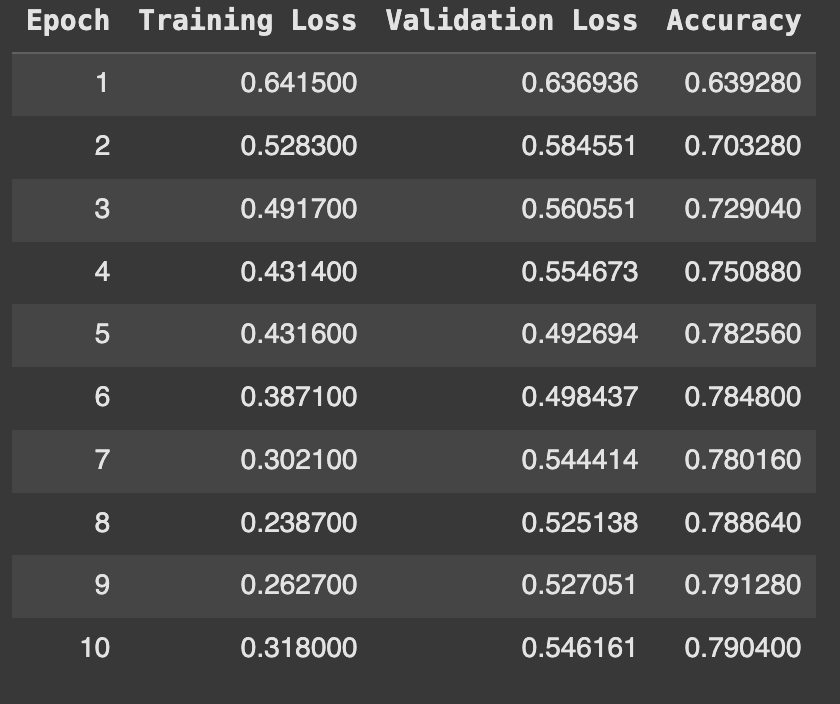Fnet-Bert-Tiny trianed on CPU - Train, validation loss and accuracy on finetuning on the IMDB dataset

Fnet-Bert-Tiny and bert-tiny (vanilla) on CPU - Training and inference time

Graphical results

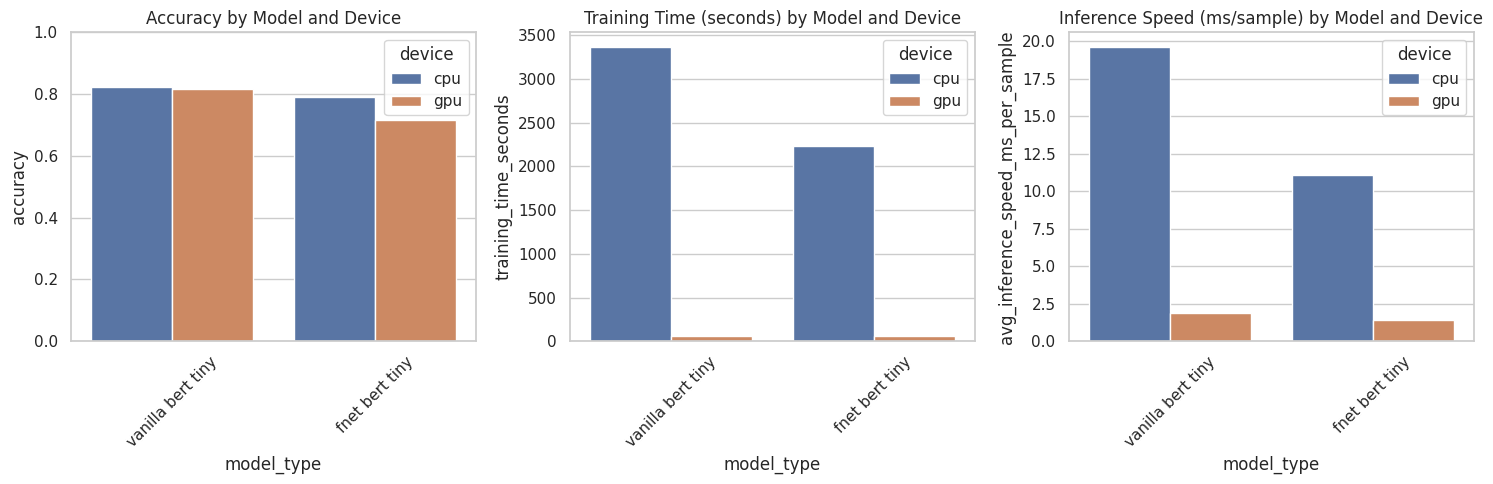Fnet-Bert-Tiny vs bert-tiny (vanilla)

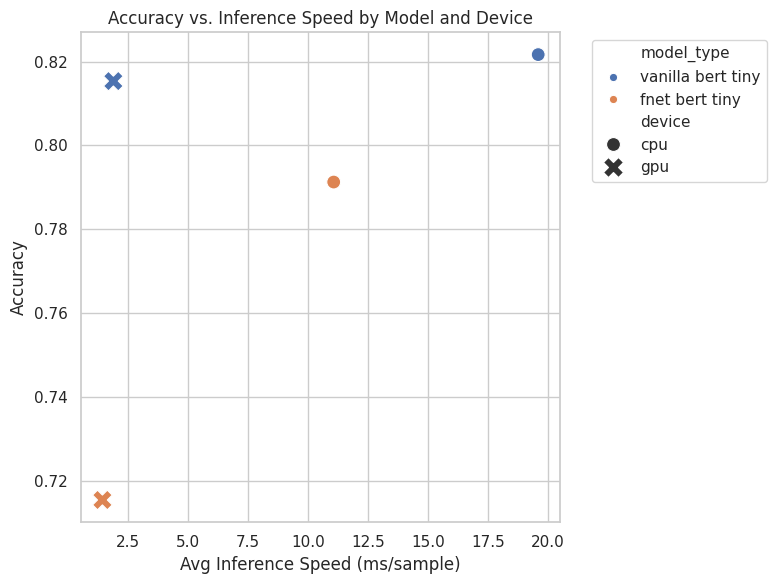Accuracy vs inference speed by model and device

Conclusion

Inference time

• on CPU fnet-bert-tiny is ~43% faster than vanilla-bert-tiny
• on GPU fnet-bert-tiny is ~24% faster than vanilla-bert-tiny

Training time

• on CPU fnet-bert-tiny trains ~33% faster than vanilla-bert-tiny
• on GPU fnet-bert-tiny trains ~9% faster than vanilla-bert-tiny

Accuracy

• on CPU fnet-bert-tiny achieves ~96% accuracy of vanilla-bert-tiny
• on GPU fnet-bert-tiny achieves ~96% accuracy of vanilla-bert-tiny

FNet variations

These are the different implemtations of fourier transformns in pytorch

Conclusion

Task specific smaller models can be viable in situations where latency needs to be low. It doesn't makes sense to use local self hosted models or even API's for simple tasks like binary classification. Fourier modified transformers (along with attention based optimizations like flash attention and paged attention) can provide additional latency cuts by optimizing the overhead computational cost.

References

1. FNet: Mixing Tokens with Fourier Transforms